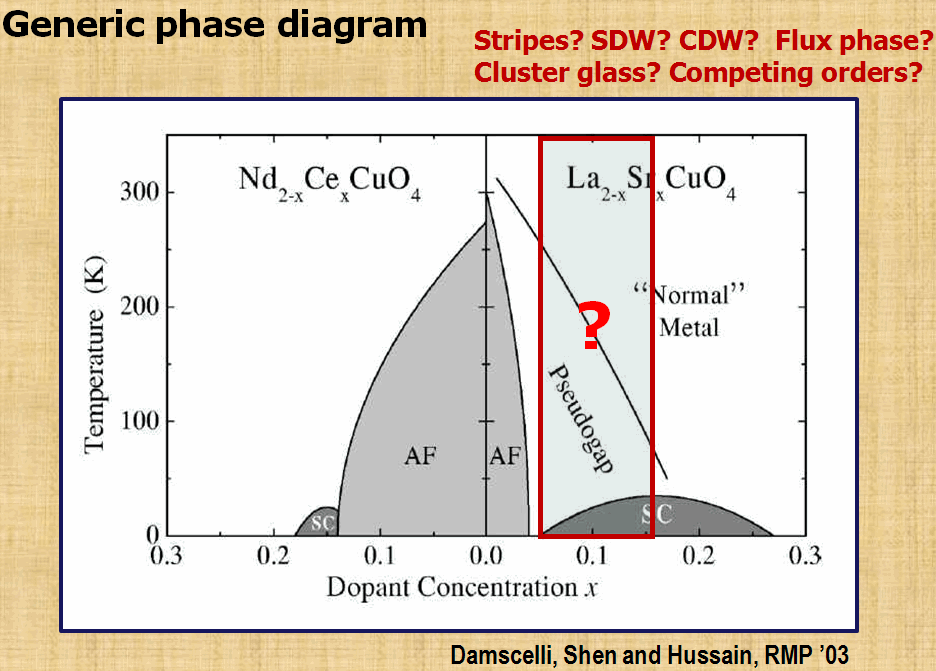
- High-Tc Superconductivity
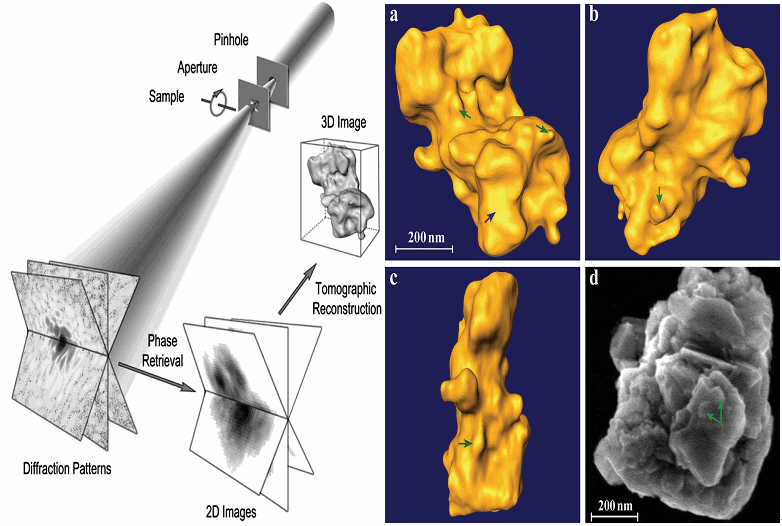
- X-ray diffraction microscopy
- Biological physics
- First-principles calculations
High-Tc Superconductivity
To search the mechanism of high-temperature superconductivity is always the most part of interests in our group. By using the variational Monte-Carlo approach and Gutzwiller's approximation, we have been trying to understand the importance of strong correlation in various experiments reported for high temperature superconductors. So far the theoretical results obtained from 2D t-J type models have been able to provide qualitative and even quantitative explanation for a number of experiements. The most recent works on stripe formation (the figure below) have again demonstrated the importance of strong correlation in getting this exotic state.
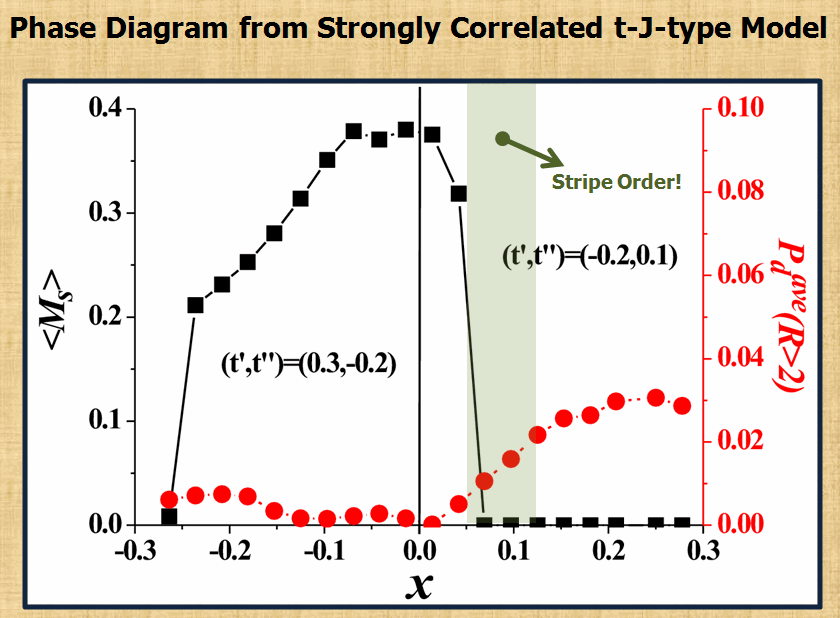
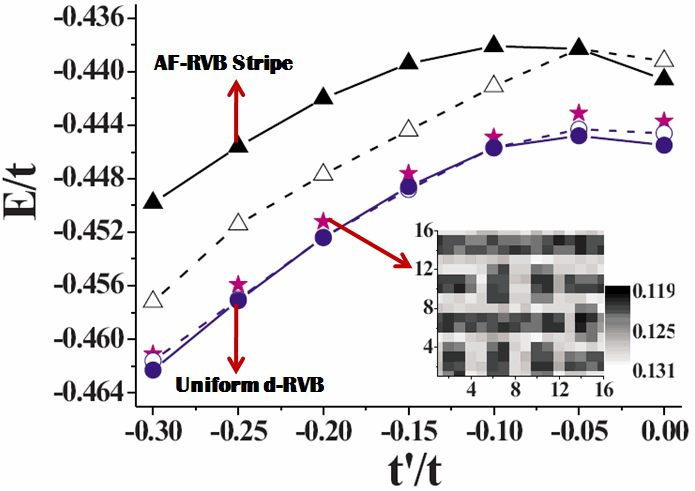
X-ray diffraction microscopy
With the advance in nanoscience and nanotechnology, x-ray diffraction microscopy, a newly developed imaging technique, is becoming more and more important in structural determination of nonperiodic micro- or nano-objects. The idea of possibly extending the methodology of x-ray crystallography to noncrystalline objects, i.e., x-ray diffraction microscopy was first suggested by Sayre in 1980. It was not until in 1999 that the first demonstration experiment was carried out by Miao et al., which was based on the oversampling phasing method. When the diffraction intensities of a finite object are sampled sufficiently finer than the Nyquist frequency so that the number of correlated intensities is more than the number of unknown variables in real space, phases are usually uniquely encoded in the diffraction intensities.
Here, we have developed an algorithm that combines the concept of optimization with the conventional hybrid input-output (HIO) algorithm for phase retrieval of oversampled diffraction intensities. In particular, the optimization algorithm of guiding searching direction to locate the global minimum has been implemented. Compared with HIO, this guided HIO (GHIO) algorithm retrieves the lost phase information from diffraction intensities with much better accuracy not only on model but also on experimental data.
Moreover, instead of traditional tomographic methods, we also developed a novel approach to reconstruct 3D image from couples of 2D projections or 2D diffraction patterns. This method combines the concepts of Pseudo-Polar Fourier transform and 3D GHIO so that it overcomes the misalignment problem and makes the reconstruction from very limit data more reliable due to perform a global optimization. So far it has been demonstrated to be a method with smallest error.
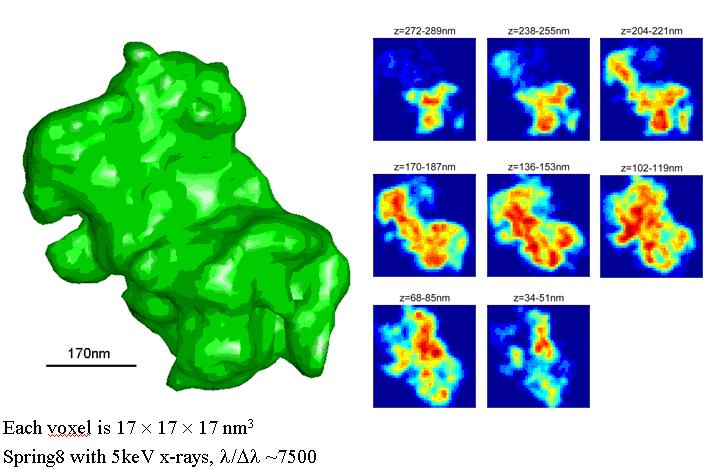
Biological physics - an automatic tracing algorithm
In recent years, numerous three-dimensional digital images were taken from confocal laser scanning microscope, X-ray and other imaging techniques for complex structures like neurons, blood vessel, collagen, fibers, etc... However, how to analyze these complex structures to obtain useful information is very challenging. One particular problem, e.g. the tracking of neuron fibers, is essential for quantitative analysis of neurons. Therefore, a very efficient tracing method is crucial and very desirable. At present there are methods and commercial software packages for this function. But it requires a viewer to use his/her vision and judgment to connect or trace the fibers. Not only the task is very labor intensive but the result is susceptible to errors and is usually lack of objectivity.
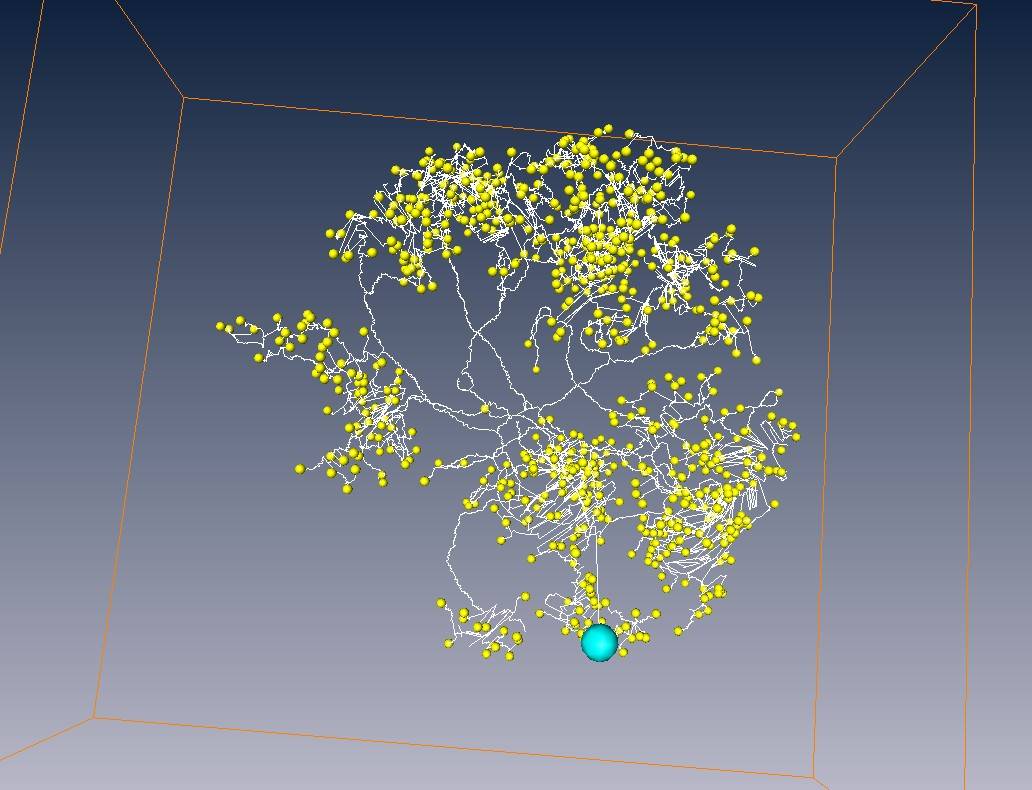
Here we report a new method developed by us which can automatically trace the image data of tree-like or network-like structures, such as neurons and blood vessels, without depending on the human intervention. All image voxels were encoded based on the idea of Huygens principle and traced via these codelets with some stopping criterions. With this method, some characteristic quantity of fibers can be found, for example, the center line, the branch points, the end points, the cross section area, and the branch angles etc¡K
A tracing result for antennal lobe local neurons in Drosophila

Neuron voxels, blue part = soma region

White line = skeleton of neuron fiber

Red points = branch points
Yellow points = end points

Yellow points = end points
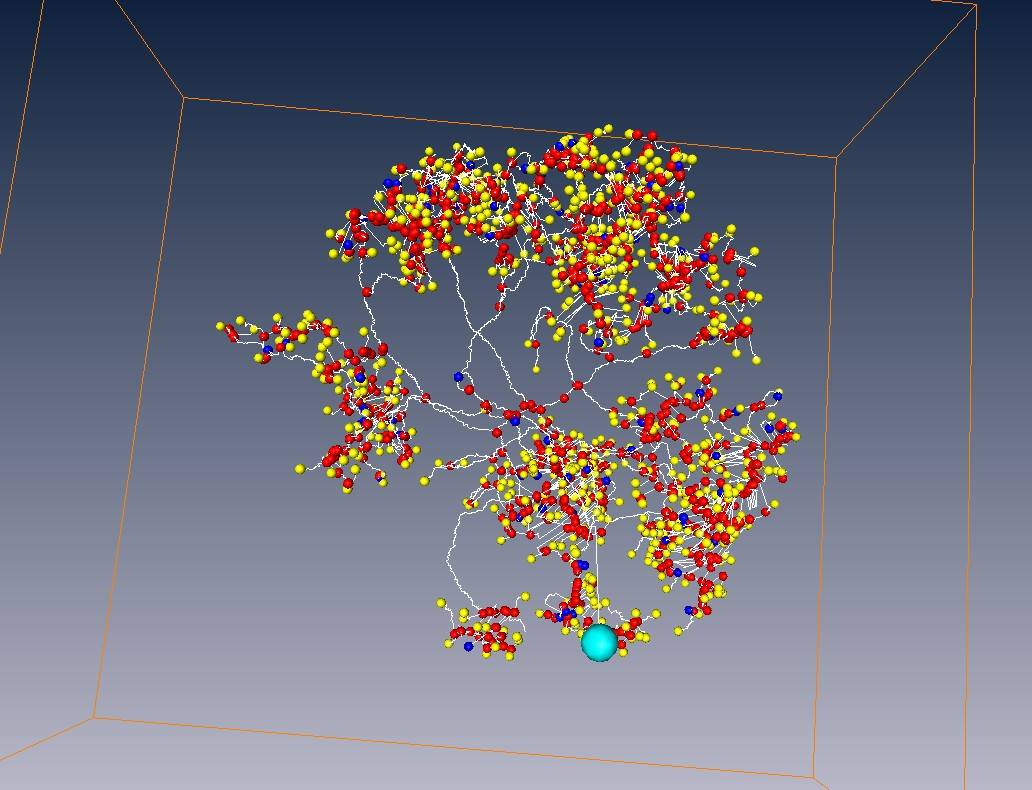
All tracing results

Tracing results with neuron voxels
![]()
